The Ouroboros model
Computer science is as much about computers as astronomy is
about telescopes.
-- Edsger Wybe Dijkstra
The model for computer networks underlying the Ouroboros prototype is the result of a long process of gradual increases in my understanding of the core principles that underly computer networks, starting from my work on traffic engineering packet-over-optical networks using Generalized Multi-Protocol Label Switching (G/MPLS) and Path Computation Element (PCE), then Software Defined Networks (SDN), the work with Sander investigating the Recursive InterNetwork Architecture (RINA) and finally our implementation of what would become the Ouroboros Prototype. The way it is presented here is not a reflection of this long process, but a crystalization of my current understanding of the Ouroboros model.
I’ll start with the very basics, assuming no delay on links and infinite capacity, and then gradually add delay, link capacity, failures, etc to assess their impact and derive what needs to be added where in order to come to the complete Ouroboros model.
The main objective of the definitions – and the Ouroboros model as a whole – is to separate mechanism (the what) from policy (the how) so that we have objective definitions and a consistent framework for reasoning about functions and protocols in computer networks.
The importance of first principles
One word of caution, because this model might read like I’m “reinventing the wheel” and we already know how to do everything that is written here. Of course we do! The point is that the model reduces networking to its essence, to its fundamental parts.
After studying most courses on Computer Networks, I could name the 7 layers of the OSI model, I know how to draw TCP 3-way handshakes, could detail 5 different TCP congestion control mechanisms, calculate optimal IP subnets given a set of underlying Local Area Networks, draw UDP headers, chain firewall rules in iptables, calculate CRC checksums, and derive spanning trees given MAC addresses of Ethernet bridges. But after all that, I still feel such courses teach about as much about computer networks as cookbooks teach about chemistry. I wanted to go beyond technology and the rote knowledge of how things work to establish a thorough understanding of why they work. During most of my PhD work at the engineering department, I spent my research time on modeling telecommunications networks and computer networks as graphs. The nodes represented some switch or router – either physical or virtual –, the links represented a cable or wire – again either physical or virtual – and then the behaviour of various technologies were simulated on those graphs to develop algorithms that analyze some behaviour or optimize some or other key performance indicator (KPI). This line of reasoning, starting from networked devices is how a lot of research on computer networks is conducted. But what happens if we turn this upside down, and develop a universal model for computer networks starting from first principles?
This sums up my problem with computer networks today: not everything in their workings can be fully derived from first principles. It also sums up why I was attracted to RINA: it was the first time I saw a network architecture as the result of a solid attempt to derive everything from first principles. And it’s also why Ouroboros is not RINA: RINA still contains things that can’t be derived from first principles.
Two types of layers
The Ouroboros model postulates that there are only 2 scalable methods of distributing packets in a network layer: FORWARDING packets based on some label, or FLOODING packets on all links but the incoming link.
We call an element that forwards a forwarding element, implementing a packet forwarding function (PFF). The PFF has as input a destination name for another forwarding element (represented as a vertex), and as output a set of output links (represented as arcs) on which the incoming packet with that label is to be forwarded on. The destination name needs to be in a packet header.
We call an element that floods a flooding element, and it implements a packet flooding function. The flooding element is completely stateless, and has a input the incoming arc, and as output all non-incoming arcs. Packets on a broadcast layer do not need a header at all.
Forwarding elements are equal, and need to be named, flooding elements are identical and do not need to be named1.

Peering relationships are only allowed between forwarding elements, or between flooding elements, but never between a forwarding element and a flooding element. We call a connected graph consisting of nodes that hold forwarding elements a unicast layer, and similary we call a connected tree2 consisting of nodes that house a flooding element a broadcast layer.
The objective for the Ouroboros model is to hold for all packet networks; our conjecture is that all scalable packet-switched network technologies can be decomposed into finite sets of unicast and broadcast layers. Implementations of unicast and broadcast layers can be easily found in TCP/IP, Recursive InterNetworking Architecture (RINA), Delay Tolerant Networks (DTN), Ethernet, VLANs, Loc/Id split (LISP),… 3. The Ouroboros model by itself is not recursive. What is known as recursive networking is a choice to use a single standard API for interacting with all the implementatations of unicast layers and a single standard API for interacting with all implementations of broadcast layers4.
The unicast layer
A unicast layer is a collection of interconnected nodes that implement forwarding elements. A unicast layer provides a best-effort unicast packet service between two endpoints in the layer. We call the abstraction of this point-to-point unicast service a flow. A flow in itself has no guarantees in terms of reliability 5.

A representation of a very simple unicast layer is drawn above, with a flow between the green (bottom left) and red (top right) forwarding elements.
The forwarding function operates in such a way that, given the label of the destination forwarding element (in the case of the figure, a red label), the packet will move to the destination forwarding element (red) in a deliberate manner. The paper has a precise mathematical definition, but qualitatively, our definition of FORWARDING ensures that the trajectory that packets follow through a network layer between source and destination
- doesn’t need to use the ‘shortest’ path
- can use multiple paths
- can use different paths for different packets between the same source-destination pair
- can involve packet duplication
- will not have non-transient loops67
The first question is: what information does that forwarding function need in order to work? Mathematically, the answer is that all forwarding elements needs to know the values of a valid distance function8 between themselves and the destination forwarding element, and between all of their neighbors and the destination forwarding element. The PFF can then select a (set of) link(s) to any of its neighbors that is closer to the destination forwarding element according to the chosen distance function and send the packet on these link(s). Thus, while the forwarding elements need to be _named_, the links between them need to be _measured_. This can be either explicit by assigning a certain weight to a link, or implicit and inferred from the distance function itself.
The second question is: how will that forwarding function know this distance information? There are a couple of different possible answers, which are all well understood. I’ll briefly summarize them here.
A first approach is to use a coordinate space for the names of the forwarding elements. For instance, if we use the GPS coordinates of the machine in which they reside as a name, then we can apply some basic geometry to calculate the distances based on this name only. This simple GPS example has pitfalls, but it has been proven that any connected finite graph has a greedy embedding in the hyperbolic plane. The obvious benefit of such so-called geometric routing approaches is that they don’t require any dissemination of information beyond the mathematical function to calculate distances, the coordinate (name) and the set of neighboring forwarding elements. In such networks, this information is disseminated during initial exchanges when a new forwarding element joins a unicast layer (see below).
A second approach is to disseminate the values of the distance function to all destinations directly, and constantly updating your own (shortest) distances from these values received from other forwarding elements. This is a very well-known mechanism and is implemented by what is known as distance vector protocols. It is also well-known that the naive approach of only disseminating the distances to neighbors can run into a count to infinity issue when links go down. To alleviate this, path vector protocols include a full path to every destination (making them a bit less scaleable), or distance vector protocols are augmented with mechanisms to avoid transient loops and the resulting count-to-infinity (e.g. Babel).
The third approach is to disseminate the link weights of neighboring links. From this information, each forwarding element can build a view of the network graph and again calculate the necessary distances that the forwarding function needs. This mechanism is implemented in so-called link-state protocols.
I will also mention MAC learning here. MAC learning is a bit different, in that it is using piggybacked information from the actual traffic (the source MAC address) and the knowledge that the adjacency graph is a tree as input for the forwarding function.
There is plenty more to say about this, and I will, but first, I will need to introduce some other concepts, most notably the broadcast layer.
The broadcast layer
A broadcast layer is a collection of interconnected nodes that house flooding elements. The node can have either, both or neither of the sender and receiver role. A broadcast layer provides a best-effort broadcast packet service from sender nodes to all (receiver) nodes in the layer.

Our simple definition of FLOODING – given a set of adjacent links, send packets received on a link in the set on all other links in the set – has a huge implication the properties of a fundamental broadcast layer: the graph always is a tree, or packets could travel along infinite trajectories with loops 9.
Building layers
We now define 2 fundamental operations for constructing packet network layers: enrollment and adjacency management. These operations are very broadly defined, and can be implemented in a myriad of ways. These operations can be implemented through manual configuration or automated protocol interactions. They can be skipped (no-operation, (nop)) or involve complex operations such as authentication. The main objective here is just to establish some common terminology for these operations.
The first mechanism, enrollment, adds a (forwarding or flooding) element to a layer; it prepares a node to act as a functioning element of the layer, establishes its name (in case of a unicast layer). In addition, it may exchange some key parameters (for instance a distance function for a unicast layer) it can involve authentication, and setting roles and permissions. Bootstrapping is a special case of enrollment for the first node in a layer. The inverse operation is called unenrollment.
After enrollment, we may add peering relationships by creating adjacencies between forwarding elements in a unicast layer or between flooding elements in a broadcast layer. This will establish neighbors and in case of a unicast layer, may addinitionally define link weights. The inverse operations is called tearing down adjacencies between elements. Together, these operations will be referred to as adjacency management.
Operations such as merging and splitting layers can be decomposed into these two operations. This doesn’t mean that merge operations shouldn’t be researched. To the contrary, optimizing this will be instrumental for creating networks on a global scale.
For the broadcast layer, we already have most ingredients in place. Now we will focus on the unicast layer.
Scaling the unicast layer
Let’s look at how to scale implementations of the packet forwarding function (PFF). On the one hand, in distance vector, path vector and link state, the PFF is implemented as a table. We call it the packet forwarding table (PFT). On the other hand, geometric routing doesn’t need a table and can implement the PFF as a mathematical equation operating on the forwarding element names. In this respect, geometric routing looks like a magic bullet to routing table scalability – it doesn’t need one – but there are many challenges relating to the complexity of calculating greedy embeddings of graphs that are not static (a changing network where routers and end-hosts enter and leave, and links can fail and return after repair) that currently make these solutions impractical at scale. We will focus on the solutions that use a PFT.
The way the unicast layer is defined at this point, the PFT scales linearly with the number of forwarding elements (n) in the layer, its space complexity is O(n)10. The obvious solution to any student of computer networks is to use a scheme like IP and Classless InterDomain Routing (CIDR) where the hosts addresses are subnetted, allowing for entries in the PFT to be aggregated, drastically reducing its space complexity, in theory at least, to O(log(n)). So we should not use arbitrary names for the forwarding elements, but give them an address!
Sure, that is the solution, but not so fast! When building a model, each element in the model should be well-defined and named at most once – synonyms for human use are allowed and useful, but they are conveniences, not part of the functioning of the model. If we subdivide the name of the forwarding element in different subnames, as is done in hierarchical addressing, we have to ask ourselves what element in the model each subname that name is naming! In the geographic routing example above, we dragged the Earth into the model, and used GPS coordinates (latitude and longitude) in the name. But where do subnets come from, and what are addresses? What do we drag into our model, if anything, to create them?
A quick recap

Let’s recap what a simple unicast layer that uses forwarding elements with packet forwarding table looks like in the model. First we have the unicast layer itself, consisting of a set of forwarding elements with defined adjacencies. Recall that the necessary and sufficient condition for the unicast layer to be able to forward packets between any (source, sink)-pair is that all forwarding engines can deduce the values of a distance function between themselves and the sink, and between each of their neighbors and the sink. This means that such a unicast layer requires an additional (optional) element that distributes this routing information. Let’s call it the Routing Element, and assume that it implements a simple link-state routing protocol. The RE is drawn as a turquoise element accompanying each forwarding element in the figure above. Now, each routing element needs to disseminate information to all other nodes in the layer, in other words, it needs to broadcast link state information. The RE is inside of a unicast layer, and unicast layers don’t do broadcast, so the REs will need the help of a broadcast layer. That is what is drawn in the figure above. Now, at first this may look weird, but an IP network does this too! For instance, the Open Shortest Path First (OSPF) protocol uses IP multicast between OSPF routers. The way that the IP layer is defined just obfuscates that this OSPF multicast network is in fact a disguised broadcast layer. I will refer to my blog post on multicast if you like a bit more elaboration on how this maps to the IP world.
Subdividing the unicast layer
Vital realizations not only provide unforeseen clarity, they also
energize us to dig deeper.
-- Brian Greene (in "Until the end of time")
Now, it’s obvious that a single global layer like this with billions of nodes will buckle under its own size, we need to split things up into smaller, more manageable groups of nodes.
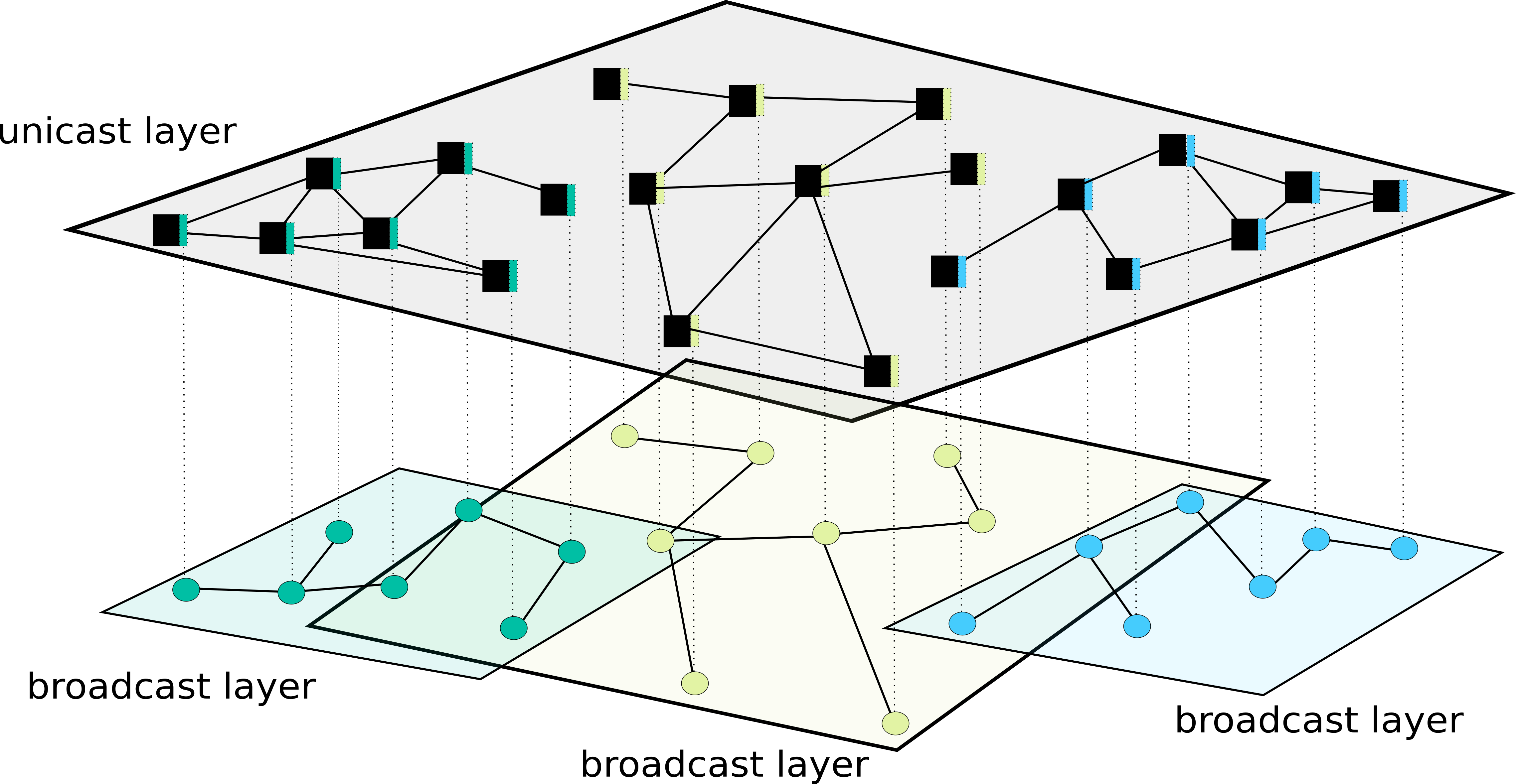
This is shown in the figure above, where the unicast layer is split into 3 groups of forwarding elements, let’s call them routing areas, a yellow, a turquoise and a blue area, with each its own broadcast layer for disseminating the link state information that is needed to populate the forwarding tables. These areas can be chosen small enough so that the forwarding tables (which still scale linear with respect to the number of participating nodes in the routing area) are manageable in size. It can also keep latency in disseminating the link-state packets in check, but we will deal with latency later, for now, let’s still assume latency on the links is zero and bandwidth on the links is infinite.
Now, in this state, there can’t be any communication between the routing areas, so we will need to add a fourth one.
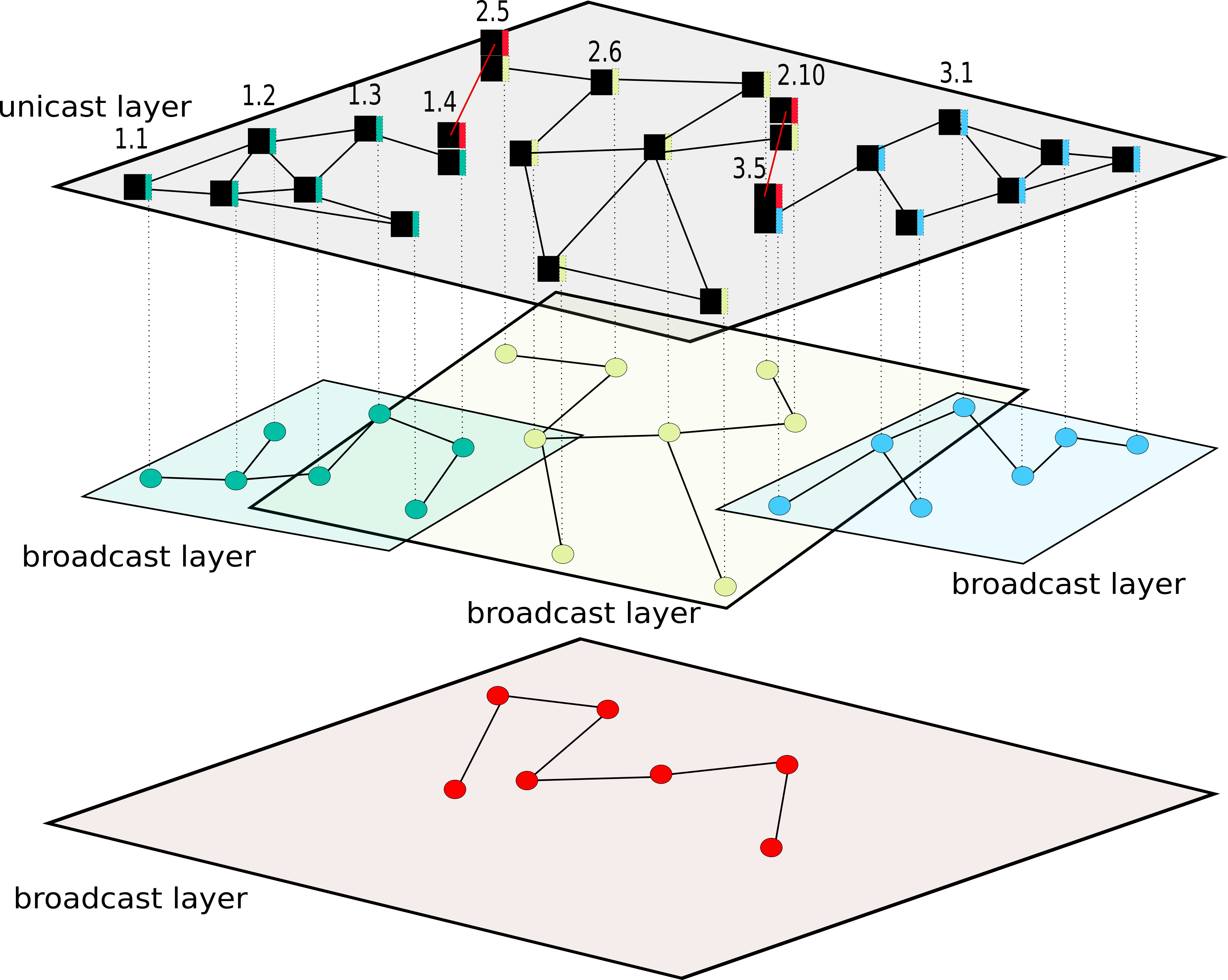
This is show in the figure above. We have our 3 original routing areas, and I numbered some of the nodes in these original routing areas. These are the numbers after the dot in figure: 1, 2, 3, 4 in the turquoise routing area, 5,6,10 in the yellow routing area, and 1, 5 in the blue area (I omitted some not to clutter the illustration).
We have also added 4 new forwarding elements, each with their own (red) routing element, that have a client-server relationship (rather than a peering relationship) with other forwarding elements in the layer. These are the numbers before the dot: 1, 2, 2, and 3. This may look intuitively obvious, and “1.4” and “3.5” may look like “addresses”, but let’s stress the things that I think are important, noting that this is a model and most certainly not an implementation design.
Every node in the unicast layer above consists of 2 forwarding elements in a client-server relationship, but all the ones that are not drawn all have the same name, and are not functionally active, but are there in a virtual way to keep the naming in the layer unique.
We did not introduce new elements to the model, but we did add a new client-server relationship between forwarding elements.
This client-server relationship gives rise to some new rules for naming the forwarding elements.
First, the names of forwarding elements that are within a routing area have to be unique within that routing area if they have no client forwarding elements within the node.
Forwarding elements with client forwarding elements have the same name if and only if their clients are within the same routing area.
In the figure, there are peering relationships between unicast nodes “1.4” and “2.5” and unicast nodes “2.10” and “3.5”, and these four nodes disseminate forwarding information using the red broadcast layer11.
Note that not all forwarding elements need to actively disseminate routing information. If the forwarding elements in the turquoise routing area were all (logically) directly connected to 1.4, they would not need the broadcast layer, this is like IP, which also doesn’t require end-hosts to run a routing protocol.
Structure of a unicast node
The rules for allowed peering relationships relate to the structure of the client-server relationship. In most generalized form, this relationship gives rise to a directed acyclic graph (DAG) between forwarding elements that are part of the same unicast node.

We call the rank of the forwarding element within the node the height at which it resides in this DAG. For instance, the figure above shows two unicast nodes with their forward elements arranged as DAGs. The forwarding elements with a turquoise and purple routing element are at rank 0, and the ones with a yellow routing element are at rank 3.
A forwarding elements in one node can have peering relationships only with forwarding elements of other nodes that
1) Are at the same rank,
2) Have a different name,
3) Are in the same routing area at that rank,
and only if
1) there are no peering relationships between two forwarding elements that are in the same unicast nodes at any forwarding element that is on a path towards the root of the DAG
2) there cannot be a lower ranked peering relationship.
So, in the figure above, there cannot be a peering relationship at rank 0, because these elements are in different routing areas (turquoise and purple). The lowest peering relationship can be at rank 1, in the routing area. If at rank one, the right node would be in a different routing area, there could be 2 peering relationships between these unicast nodes, for instance at rank 2 in the green routing area, and at rank 3 between in the yellow routing area (or also at rank 2 in the blue routing area).
What are addresses?
Let’s end this discussion with how all this relates to IP addressing and CIDR. Each “IPv4” host has 32 forwarding elements with a straight parent-child relationship between them 12. The rules above imply that there can be only one peering relationship between two nodes. The subnet mask actually acts as a sort of short-hand notation, showing where the routing elements are in the same routing area: with mask 255.255.255.0, the peering relationship is at rank 8, IP network engineers then state that the nodes are in a /24 network.
Apart from building towards CIDR from the ground up, we have also derived what network addresses really are: they consist of names of forwarding elements in a unicast node and reflect the organisation of these forwarding elements in a directed acyclic graph (DAG). Now, there is still a (rather amusing) and seemingly neverending discussion in the network community on whether IP adresses should be assigned to nodes or interfaces. This discussion is moot: you can write your name on your mailbox, that doesn’t make it the name of your mailbox, it is your name. It is also a false dichotomy caused by device-oriented thinking, looking at a box of electronics with a bunch of holes in which to plug some wires, and then thinking that we either have to name the box or the holes: the answer is neither. Just like a post office building doesn’t do anything without post office workers (or their automated robotic counterparts), a router or switch doesn’t do anything without forwarding elements. I will come back to this when discussing multi-homing.
One additional thing is that in the current IP Internet, the layout of the routing areas is predominantly administratively defined and structured into so-called Autonomous Systems (ASs) that each receive a chunk of the available IP address space, with BGP used to disseminate routes between them. The layout and peering relationship between these ASs is not the most optimal for the layout of the Internet. Decoupling the network addressing within an AS from the addressing and structure of an overlaying unicast layer, and how to disseminate routes in that overlay unicast layer is an interesting topic that mandates more study13.
Do we really need routing at a global scale?
An interesting question to ask, is whether we need to be able to scale a layer to the scale of the planet, or – some day – the solar system, or even the universe? IPv6 was the winning technology to deal with the anticapted problem of IPv4 address exhaustion. But can we build an Internet that doesn’t require all possible end users to share the same network (layer)?
My answer is not proven and therefore not conclusive, but I think yes, any public Internetwork at scale – where it is possible for any end-user to reach any application – will always need at least one (unicast) layer that spans most of the systems on the network and thus a global address space. In the current Internet, applications are identified by an IP address and (well-defined) port, and the Domain Name System (DNS) maps the host name to an IP address (or a set of IP addresses). In any general Internetwork, if applications were in private networks, we would need a system to find the (private network, node name in private network) for some application, and every end-host would need to reach that system, which – unless I am missing something big – means that system will need a global address space14.
Multi-homing
[Under construction - this blog post over Loc/ID split might be interesting]
Dealing with limited link capacity
[Under construction]
In the paper we call these elements data transfer protocol machines, but I think this terminology is clearer.
[return]- A tree is a connected graph with N vertices and N-1 edges. [return]
I’ve already explored how some technologies map to the Ouroboros model in my blog post on unicast vs multicast.
[return]Of course, once the model is properly understood and a green-field scenario is considered, recursive networking is the obvious choice, and so the Ouroboros prototype is a recursive network.
[return]This is where Ouroboros is similar to IP, and differs from RINA. RINA layers (DIFs) aim to provide reliability as part of the service (flow). We found this approach in RINA to be severely flawed, preventing RINA to be a universal model for all networking and IPC. RINA can be modeled as an Ouroboros network, but Ouroboros cannot be modeled as a RINA network. I’ve written about this in more detail about this in my blog post on Ouroboros vs RINA.
[return]Transient loops are loops that occur due to forwarding functions momentarily having different views of the network graph, for instance due to delays in disseminating information on unavailable links.
[return]Some may think that it’s possible to build a network layer that forwards packets in a way that deliberately takes a couple of loops between a set of nodes and then continues forwarding to the destination, violating the definition of FORWARDING. It’s not possible, because based on the destination address alone, there is no way to know whether that packet came from the loop or not. “But if I add a token/identifier/cookie to the packet header” – yes, that is possible, and it may look like that packet is traversing a loop in the network, but it doesn’t violate the definition. The question is: what is that token/identifier/cookie naming? It can be only one of a couple of things: a forwarding element, a link or the complete layer. Adding a token and the associated logic to process it, will be equivalent to adding nodes to the layer (modifying the node name space to include that token) or adding another layer. In essence, the implementation of the nodes on the loop will be doing something like this:
if logic_based_on_token: # behave like node (token, X) else if logic_based_on_token: # behave like node (token, Y) else # and so onWhen taking the transformation into account the resulting layer(s) will follow the fundamental model as it is presented above. Also observe that adding such tokens may drastically increase the address space in the ouroboros representation.
[return]For the mathematically inclined, the exact formulation is in the paper section 2.4
[return]Is it possible to broadcast on a non-tree graph by pruning in some way, shape or form? There are some things to consider. First, if the pruning is done to eliminate links in the graph, let’s say in a way that STP prunes links on an Ethernet or VLAN, then this is operation is equivalent creating a new broadcast layer. We call this enrollment and adjacency management. This will be explained in the next sections. Second is trying to get around loops by adding the name of the (source) node plus a token/identifier/cookie as a packet header in order to detect packets that have traveled in a loop, and dropping them when they do. This kind of network doesn’t fit neither the broadcast layer nor the unicast layer. But the thing is: it also doesn’t scale, as all packets need to be tracked, at least in theory, forever. Assuming packet ordering is preserved inside a layer a big no-no. Another line of thinking may be to add a decreasing counter to avoid loops, but it goes down a similar rabbit hole. How large to set the counter? This also doesn’t scale. Such things may work for some use cases, but they don’t work in general.
[return]In addition to the size of the packet forwarding tables, link state, path vector and distance vector protocols are also limited in size because of time delays in disseminating link state information between the nodes, and the amount to be disseminated. We will address this a bit later in the discourse.
[return]The functionality of this red routing element is often implemented as an unfortunate human engineer that has to subject himself to one of the most inhuman ordeals imaginable: manually calculating and typing IP destinations and netmasks into the routing tables of a wonky piece of hardware using the most ill-designed command line interface seen this side of 1974.
[return]Drawing this in a full network example is way beyond my artistic skill.
[return]There is a serious error in the paper that states that this routing information can be marked with a single bit. This is only true in the limited case that there is only one “gateway” node in the routing area. In the general case, path information will be needed to determine which gateway to use.
[return]A paper on RINA that claims that a global address space is not needed, seems to prove the exact opposite of that claim. The resolution system, called the Inter-DIF Directory (IDD) is present on every system that can make use of it and uses internal forwarding rules based on the lookup name (in a hierarchical namespace!) to route requests between its peer nodes. If that is not a global address space, then I am Mickey Mouse: the addresses inside the IDD are just based on strings instead of numbers. The IDD houses a unicast layer with a global address space. While the IDD is techically not a DIF, the DIF-DAF distinction is severely flawed.
[return]